In Which Situations Would You Expect Changes In The Genetic Makeup Of A Population?

Natural pick, genetic drift, and factor flow are the mechanisms that cause changes in allele frequencies over time. When i or more of these forces are acting in a population, the population violates the Hardy-Weinberg assumptions, and evolution occurs. The Hardy-Weinberg Theorem thus provides a null model for the study of evolution, and the focus of population genetics is to understand the consequences of violating these assumptions.

Natural choice occurs when individuals with certain genotypes are more likely than individuals with other genotypes to survive and reproduce, and thus to laissez passer on their alleles to the next generation. Every bit Charles Darwin (1859) argued in On the Origin of Species, if the post-obit conditions are met, natural selection must occur:

1. At that place is variation among individuals within a population in some trait.
2. This variation is heritable (i.e., there is a genetic basis to the variation, such that offspring tend to resemble their parents in this trait).
3. Variation in this trait is associated with variation in fitness (the average net reproduction of individuals with a given genotype relative to that of individuals with other genotypes).

Directional selection leads to increase over time in the frequency of a favored allele. Consider three genotypes (AA, Aa and aa) that vary in fettle such that AA individuals produce, on average, more offspring than individuals of the other genotypes. In this example, bold that the selective authorities remains abiding and that the action of selection is the only violation of Hardy-Weinberg assumptions, the A allele would become more common each generation and would eventually become fixed in the population. The rate at which an advantageous allele approaches fixation depends in function on the dominance relationships among alleles at the locus in question (Effigy 1). The initial increase in frequency of a rare, advantageous, dominant allele is more rapid than that of a rare, advantageous, recessive allele considering rare alleles are institute mostly in heterozygotes. A new recessive mutation therefore can't be "seen" by natural selection until it reaches a loftier enough frequency (maybe via the random effects of genetic drift — see below) to get-go appearing in homozygotes. A new dominant mutation, however, is immediately visible to natural selection because its effect on fitness is seen in heterozygotes. Once an advantageous allele has reached a loftier frequency, deleterious alleles are necessarily rare and thus generally present in heterozygotes, such that the final approach to fixation is more than rapid for an advantageous recessive than for an advantageous ascendant allele. As a consequence, natural pick is not as effective as one might naively expect it to be at eliminating deleterious recessive alleles from populations.

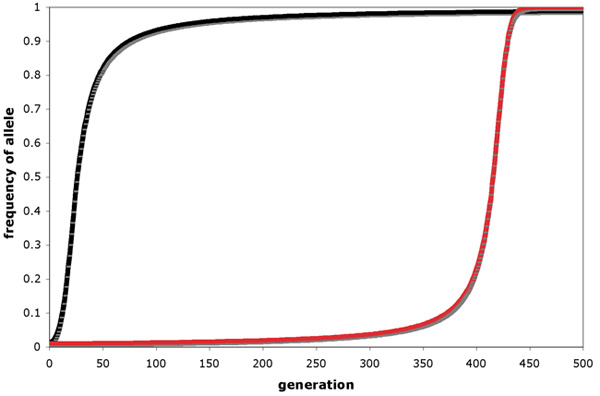
Figure 1: Allele-frequency change under directional choice favoring (a) a dominant advantageous allele and (b) a recessive advantageous allele

Balancing selection, in contrast to directional selection, maintains genetic polymorphism in populations. For example, if heterozygotes at a locus have higher fitness than homozygotes (a scenario known as heterozygote advantage or overdominance), natural selection will maintain multiple alleles at stable equilibrium frequencies. A stable polymorphism can also persist in a population if the fitness associated with a genotype decreases equally that genotype increases in frequency (i.e., if there is negative frequency-dependent selection). It is of import to notation that heterozygote disadvantage (underdominance) and positive frequency-dependent selection can too human action at a locus, only neither maintains multiple alleles in a population, and thus neither is a form of balancing selection.

Genetic drift results from the sampling error inherent in the manual of gametes past individuals in a finite population. The gamete pool of a population in generation t is the total pool of eggs and sperm produced by the individuals in that generation. If the gamete pool were infinite in size, and if there were no selection or mutation acting at a locus with ii alleles (A and a), we would wait the proportion of gametes containing the A allele to exactly equal the frequency of A, and the proportion of gametes containing a to equal the frequency of a. Compare this situation to tossing a fair coin. If you were to toss a money an space number of times, the proportion of heads would be 0.fifty, and the proportion of tails would be 0.l. If you toss a coin merely 10 times, however, you shouldn't be too surprised to become seven heads and 3 tails. This difference from the expected caput and tail frequencies is due to sampling error. The more times you lot toss the coin, the closer these frequencies should come to 0.50 considering sampling error decreases as sample size increases.

In a finite population, the adults in generation t will pass on a finite number of gametes to produce the offspring in generation t + one. The allele frequencies in this gamete pool volition generally deviate from the population frequencies in generation t because of sampling error (again, assuming there is no choice at the locus). Allele frequencies will thus change over time in this population due to chance events — that is, the population will undergo genetic drift. The smaller the population size (N), the more important the effect of genetic drift. In practice, when modeling the effects of drift, we must consider effective population size (N_e ), which is essentially the number of breeding individuals, and may differ from the census size, North, nether various scenarios, including unequal sex ratio, certain mating structures, and temporal fluctuations in population size.

At a locus with multiple neutral alleles (alleles that are identical in their furnishings on fitness), genetic drift leads to fixation of one of the alleles in a population and thus to the loss of other alleles, such that heterozygosity in the population decays to zero. At whatever given time, the probability that one of these neutral alleles will somewhen exist fixed equals that allele's frequency in the population. We can think about this issue in terms of multiple replicate populations, each of which represents a deme (subpopulation) within a metapopulation (collection of demes). Given x finite demes of equal N_e , each with a starting frequency of the A allele of 0.5, we would expect eventual fixation of A in 5 demes, and eventual loss of A in 5 demes. Our observations are likely to deviate from those expectations to some extent because we are because a finite number of demes (Figure 2). Genetic drift thus removes genetic variation within demes but leads to differentiation amid demes, completely through random changes in allele frequencies.

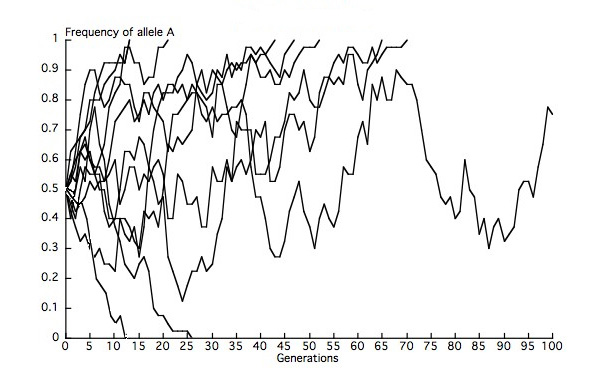
Figure ii: Simulations of allele-frequency change in 10 replicate populations (Due north = 20)

Since the initial frequency of the A allele = 0.five, nosotros expect A to be stock-still in five populations and lost in v populations, but our observations deviate from expectations because of the finite number of populations. In this run of simulations, we run across 7 instances of fixation (p = 1), 2 instances of loss (p = 0), and one instance in which there are still ii alleles later 100 generations. In this final population, A would somewhen accomplish fixation or loss.

Gene flow is the motion of genes into or out of a population. Such motility may be due to migration of individual organisms that reproduce in their new populations, or to the movement of gametes (e.g., as a consequence of pollen transfer amid plants). In the absence of natural selection and genetic drift, factor flow leads to genetic homogeneity among demes inside a metapopulation, such that, for a given locus, allele frequencies volition attain equilibrium values equal to the average frequencies across the metapopulation. In contrast, restricted gene flow promotes population departure via choice and drift, which, if persistent, can atomic number 82 to speciation.

Natural pick, genetic drift and factor menses practice not act in isolation, so we must consider how the interplay among these mechanisms influences evolutionary trajectories in natural populations. This issue is crucially important to conservation geneticists, who grapple with the implications of these evolutionary processes as they design reserves and model the population dynamics of threatened species in fragmented habitats. All real populations are finite, and thus subject to the effects of genetic migrate. In an space population, we wait directional selection to somewhen fix an advantageous allele, but this will not necessarily happen in a finite population, because the furnishings of drift tin can overcome the effects of choice if selection is weak and/or the population is small. Loss of genetic variation due to drift is of particular concern in small, threatened populations, in which fixation of deleterious alleles can reduce population viability and raise the gamble of extinction. Even if conservation efforts boost population growth, low heterozygosity is probable to persist, since bottlenecks (periods of reduced population size) have a more pronounced influence on Ne than periods of larger population size.

Nosotros have already seen that genetic migrate leads to differentiation among demes within a metapopulation. If we presume a simple model in which individuals have equal probabilities of dispersing amidst all demes (each of effective size Due north_e ) inside a metapopulation, then the migration charge per unit (m) is the fraction of cistron copies within a deme introduced via immigration per generation. According to a usually used approximation, the introduction of merely 1 migrant per generation (Northward_{due east} m = one) constitutes sufficient factor period to counteract the diversifying furnishings of genetic migrate in a metapopulation.

Natural selection tin produce genetic variation among demes within a metapopulation if unlike selective pressures prevail in different demes. If N_e is big enough to discount the effects of genetic drift, and so nosotros expect directional option to fix the favored allele within a given focal deme. However, the continual introduction, via gene flow, of alleles that are advantageous in other demes but deleterious in the focal deme, can annul the furnishings of option. In this scenario, the deleterious allele volition remain at an intermediate equilibrium frequency that reflects the balance between factor flow and natural selection.

Source: https://www.nature.com/scitable/knowledge/library/natural-selection-genetic-drift-and-gene-flow-15186648/

Posted by: smithnalled.blogspot.com

Share this post